インフォーメーション・サービス５２

最適消費の計算問題の解き方

　消費者の消費者均衡点の購入を、最適消費という。消費者の効用関数、消費者の所得、そして財の価格が与えられた場合に、最適消費の購入量を計算して求めることができる。

　ある消費者の効用関数を、U=xyとする。Uは、効用を示し、ｘはX財の消費量を示し、ｙはY財の消費量を示すとする。また、X財の価格を１０円とし、Y財の価格を２０円とする。そして、この消費者の所得を千円とする。このとき、予算制約線は、次式のとおりである。

１０ｘ＋２０ｙ＝１０００

変形すると、

ｙ＝−（１／２）ｘ＋５０・・・（１）

となる。

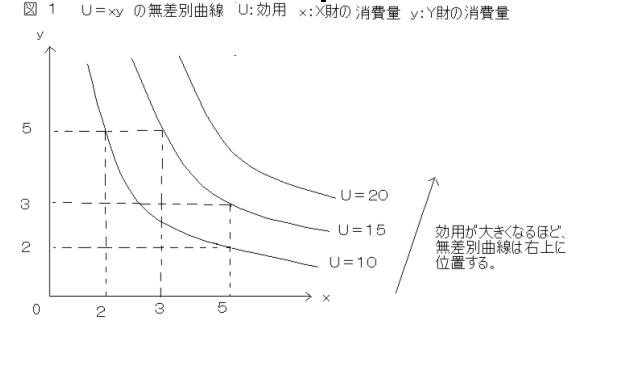
　さて、この効用関数を、図示すると図１のようになる。各効用の値に応じ、無差別曲線が図１のように描ける。効用が大きくなるほど、無差別曲線は右上に位置する。

　消費者均衡点では、予算制約線と無差別曲線が接している。それゆえ、予算制約線上の両財の消費量の組み合わせのうち、最大効用となる組み合わせが、消費者均衡点の組み合わせであり、最適消費量である。この両財の組み合わせは､次のように求めることができる。

（１） 式を、効用関数に代入して、

　　Ｕ＝ｘ｛−（１／２）ｘ＋５０｝＝−（１／２）ｘ^２＋５０ｘ

　　　＝−（１／２）（ｘ−５０）^２＋１２５０

つまり、ｘ＝５０で効用は最大となる。ｘ＝５０を（１）式に代入して、

　　ｙ＝―（１／２）×５０＋５０＝２５

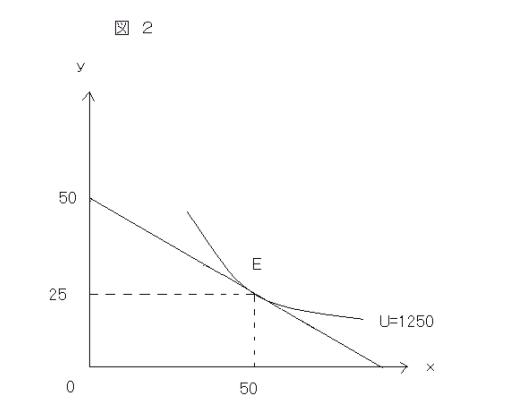
となる。よって、ｘ＝５０、ｙ＝２５で、最適消費となる。これを図で示すと、図２のとおりとなる。点Ｅが消費者均衡点である。

以上の解説を参考にして、以下の問題を解きなさい。

　問題１　ある消費者の効用関数が、Ｕ＝ｘｙ、Ｘ財の価格を５円、Ｙ財の価格を２円とする。また、この消費者の所得を１００円とすると、最適消費となる両財の消費量はいくらか。

	ｘ	ｙ
１	１０	２０
２	１０	２５
３	１５	２５
４	１５	３０
５	２０	３０

　問題２　ある消費者の効用関数が、Ｕ＝５ｘｙ，Ｘ財の価格を２０円、Ｙ財の価格を２円とする。また、この消費者の所得を２００円とすると、最適消費となる両財の消費量はいくらか。

	ｘ	ｙ
１	５	５０
２	５	６０
３	１０	６０
４	１０	７０
５	１６	７０